Latihan Algoritma Metode Iterative (Gauss-Seidel vs Jacobi)

Halo Semua.... Hari ini saya akan membahas apa yang sudah saya pelajari tentang Metode Gauss-Seidel dan Jacobi untuk menyelesaikan sebuah persamaan linear. Kedua metode di atas merupakan salah satu metode iterasi yang sudah dibahas di post sebelumnya.

Oke, langsung aja ya buka Visual Basicnya!!!

1. Buatlah userform seperti ini :

2. Untuk perintah Clear All dan Close bisa dilihat pada posting-posting sebelumnya.

3. Kemudian masukkan perintah-perintah pada cmdgauss dan cmd jacobi.

Untuk Jacobi, perbedaannya ada pada coding berikut, mengapa cuma segini?? nanti dibahas pada penjelasan algoritmanya ya.,,

3. Yuk Kita Test Hasil Pekerjaan saya...

Alhamdulillah bisa....

Berikut Penjelasan Algoritmanya.. :

1. Diketahui persamaan aljabar simultan untuk mencari nilai-nilai x1, x2, x3 dan x4.
2. nilai batas toleransi error adalah 1.11 x 10^-15. ini dicari agar metode Gauss-Seidel dan Jacobi menjadi konvergen ketika nilai error metode (c) < nilai batas toleransi (e)
3. Untuk metode Gauss-Seidel :
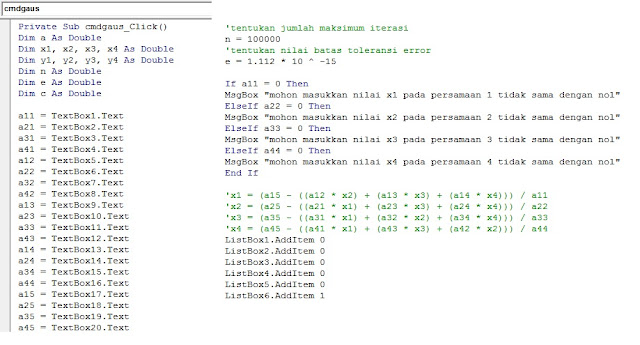
cmdgauss.
nilai x1,x2,x3 dan x4 dibuat persamaan baru.
contoh : ax1 + bx2 + cx3 + dx4 = e
x1 = e/a - bx2/a - cx3/a - dx4/a

x2 = e/b - ax1/b - cx3/b - dx4/b
x3 = e/c - ax1/c - bx2/c - dx4/c
x4 = e/d - ax1/d - bx2/d- cx3/d

iterasi 1 :

nilai x1 dicari dengan pendekatan awal nilai x2, x3 dan x4 adalah 0.
nilai x2 dicari dengan pendekatan awal nilai x1 = x1 yang di atas. Lalu x2, x3 dan x4 adalah 0
nilai x3 dicari dengan pendekatan awal nilai x1 = x1, x2 = x2 yang di atas. Lalu x3 dan x4 adalah 0
nilai x4 dicari dengan pendekatan awal nilai x1 = x1, x2 = x2, x3 = x3 yang di atas.

kemudian simpan nilai x1 = y1 begitu seterusnya.


iterasi 2 :
nilai x1 dicari dengan diketahui nilai x2, x3, dan x4 di iterasi 1.

nilai x2 dicari dengan diketahui nilai x1 pada iterasi kedua. Lalu x3 dan x4 di iterasi 1.
nilai x3 dicari dengan diketahui nilai x1 dan x2 pada iterasi kedua. Lalu x4 di iterasi 1.


nilai x4 dicari dengan diketahui nilai x1, x2, x3 pada iterasi kedua. Lalu x4 di iterasi 1.

nilai c sebagai nilai error (dicari dengan akar dari ((x1-y1)^2 + (x2-y2)^2 + (x3-y3)^2 + (x4-y4)^2)

kemudian simpan nilai x1 = y1 begitu seterusnya.



iterasi 3 :
fungsi for.
jika nilai error (c) sudah lebih kecil dari batas toleransi (e). Maka :
nilai x1, x2, x3, dan x4 sudah konvergen dan muncul pada TextBox.
jika belum, maka iterasi berulang seperti iterasi 2 dst. hingga nilai c < e.

4. Untuk metode Jacobi, sama seperti Gauss-Seidel. perbedaannya pada pendekatan awal, di mana nilai x1, x2, x3, dan x4 semuanya nol.
contoh : ax1 + bx2 + cx3 + dx4 = e
x1 = e/a
x2 = e/b
x3 = e/c
x4 = e/d

Analisis :
Metode Gauss-Seidel dan Jacobi hampir mirip. Perbedaannya tidak terlalu signifikan dan jumlah iterasi Jacobi hanya sedikit lebih banyak dari Gauss-Seidel.


Sekian, semoga bermanfaat...